逻辑回归(Logistics Regression, LR)

逻辑回归可以用来完成分类任务，适合用来做如：物体分类、垃圾邮件检测等。

要说逻辑回归，我们得追溯到线性回归，想必大家对线性回归都有一定的了解，即对于多维空间中存在的样本点，我们用特征的线性组合去拟合空间中点的分布和轨迹。如下图所示：

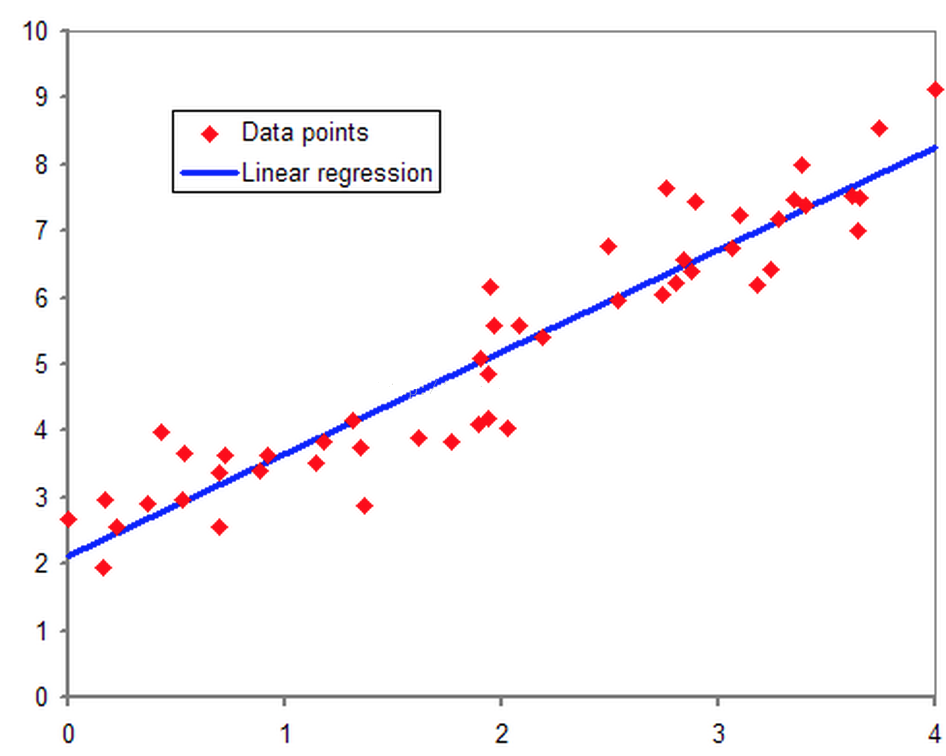
既然逻辑回归是解决分类问题，那么为什么要叫回归呢？ 逻辑回归就是用回归的办法来做分类。

考虑最简单的二分类,结果是正例或者负例的任务，按照线性回归的思路，我们可以先对这个任务进行线性回归，找出事务的规律。比如根据人的饮食、作息、工作和生存环境等条件预测一个人“有”或者“没有”得恶性肿瘤。可以先通过回归任务来预测人体内肿瘤的大小,取一个平均值作为阈值，如平均值为y，肿瘤大小超过y为恶心肿瘤，无肿瘤或大小小于y的为非恶性。这样通过线性回归加设定阈值的办法，就可以完成一个简单的二分类任务。如下图:

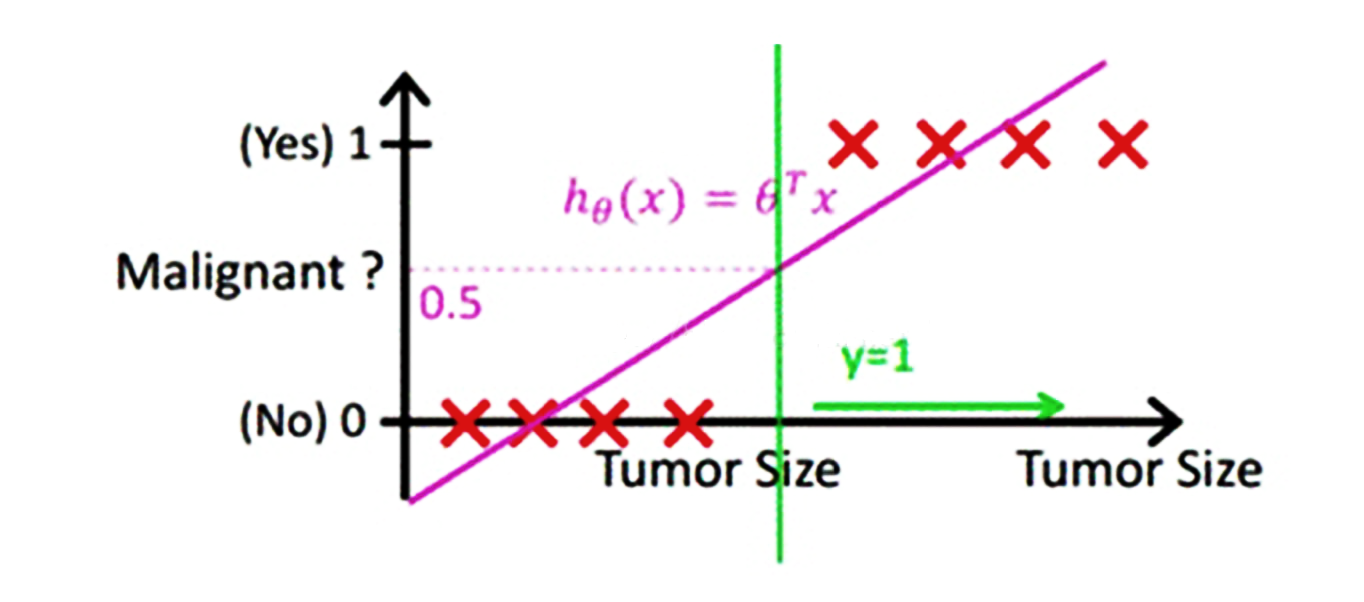
上图中，红色的x轴为肿瘤大小，粉色的线为回归函数拟合图像，绿色的线为阈值。

预测肿瘤大小还是一个回归问题，得到的结果(肿瘤的大小)也是一个连续型变量。通过设定阈值，就成功将回归问题转化为了分类问题。

但是这样做还存在一个问题，我们上面的假设，依赖于所有的肿瘤大小都不会特别离谱，如果有一个超大的肿瘤在我们的例子中，阈值就很难设定。如果还是取平均大小为阈值，则会出现下图的情况：

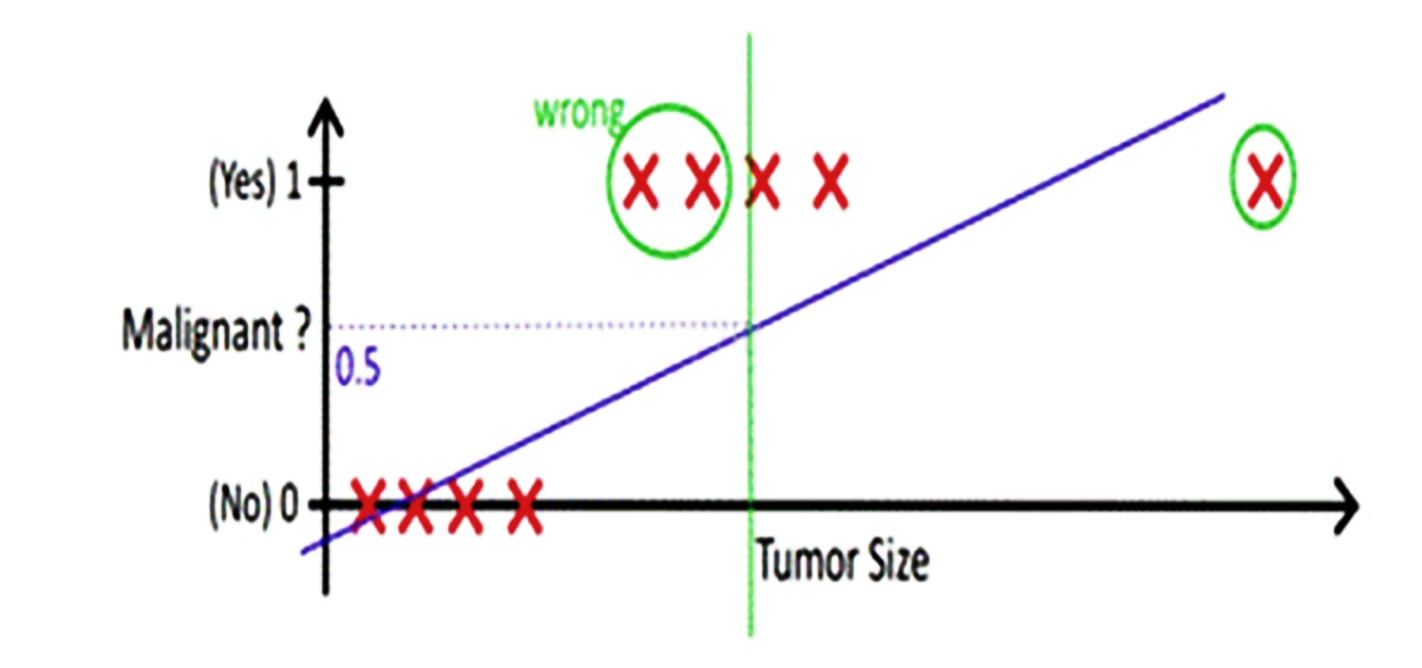
从上边的例子可以看出，使用线性的函数来拟合规律后取阈值的办法是不行的，原因在于拟合的函数是线性的直线。离群值（也叫异常值）对结果的影响过大，但是我们的整体思路是没有错的，错的是用了太“直”的拟合函数。

在这样的场景下，逻辑回归就诞生了。它的核心思想是，如果线性回归的结果输出是一个连续值，而值的范围是无法限定的，那我们有没有办法把这个结果值映射为可以帮助我们判断的结果呢？而如果输出结果是0到1之间的一个概率值，这个问题就很清楚了。 逻辑回归常用到的映射函数为sigmoid（也叫逻辑斯谛函数，是一个二分类概率函数），函数图像和公式如下图所示：

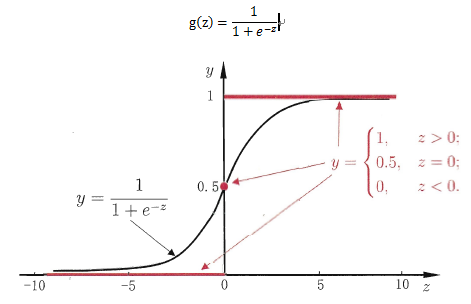
这样一个函数使得上面的例子不再像线性回归函数一样受离群值影响，因为他的输出结果是样本预测为正例或负例的概率(0到1之间的小数)。

从函数图上可以看出，函数y = g(z)在z = 0时为1/2，随着z逐渐变小，函数值趋于0，z逐渐变大时函数值趋于1。 如果定义线性回归的预测函数为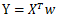，那么逻辑回归的输出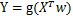，其中 y= g(z)正是上述sigmoid函数。

直观地在二维空间理解逻辑回归，sigmoid函数的特性使得判定的阈值能够映射为平面的一条判定边界，当然随着特征的复杂化，判定边界可能是多种多样的样貌，但是它能够较好地把两类样本点分隔开，解决分类问题。

求解逻辑回归参数的传统方法是梯度下降，构造为凸函数的代价函数后，每次沿着偏导方向（下降速度最快方向）迈进一小部分，直至N次迭代后到达最低点。

选定阈值

什么是选定阀值？例如我选定一个阀值为0.5，那么小于0.5的一定是负例，哪怕他是0.49。其实不一定，因为它还是有49%的概率为正利的。 但是即便他是正例的概率为0.1，我们随机选择1万个样本来做预测，还是会有接近100个预测的结果是负例，但其实应该是正例。无论我们怎么选，误差都是存在的。所以我们选定阈值的时候就是在选择可以接受误差的程度。

sigmod函数预测结果为一个0到1之间的小数，如果将阈值选作0.5可能感觉是最舒服的。可如果例子是上面做一个肿瘤的良恶性判断，阈值为0.5就意味着一个患者得恶性肿瘤的概率为0.49，模型依旧认为他没有患恶性肿瘤，结果可能就容易造成严重的医疗事故。此类情况我们应该将阈值设置的小一些。假如设置为0.3，一个人患恶性肿瘤的概率超过0.3我们的算法就会报警，造成的结果就是这个人会做一次全面检查，比起医疗事故来讲显然这个更容易接受。

第二种情况，如识别验证码，输出的概率为这个验证码识别正确的概率。此时我们大可以将概率设置的高一些，因为即便识别错了造成的结果就是程序会重试一次不同的验证码，机器识别验证码错误率本身就很高，结果显然也很容易接受。

所以阀值的选定需要根据具体场景做出合理的设定。

优缺点分析

优点：

• 实现简单，广泛应用于工业界。

• 输出结果并不是一个离散值或确切的类型，而是一个与每个输入样本相关的概率列表，这样我们可以任意设定阈值，从而得到我们想要的分类输入。

• LR对数据中的小噪音的鲁棒性很好，并且轻微的多重共线性不会对其结果产生特别的影响。严重的多重共线性可以使用LR+l2正则来解决。

缺点：

• 当样本量很大时，LR的性能并不是很好。

• 不能很好的处理大量的多类特征和变量。

• 容易欠拟合

• 传统的LR只能处理二分类，在此基础上衍生的Softmax才能处理多分类。

• 对于非线性特征，需要进行转换。

至此已经了解了逻辑回归是什么了。

多分类函数softmax

上面解释了sigmoid，输出范围为0到1之间的一个概率值，所以可以用作输出层。sigmoid函数常用于二分分类问题。例如在辨别一张图片是否为狗的问题中，将一张图片的特征向量输入神经网络，在输出层设置一个节点并使用sigmoid函数，结果会输出一个概率，根据这个概率就能辨别出图片是否为狗的图片。

对于多类分类问题即输出多个概率的问题，sigmoid函数就不符合了。这里就要介绍softmax函数了。

举个例子，建立一个模型，要分别输出为猫，狗和猪的概率。基于种种特征输入，现在猫与狗和猪得到的分数分别是2，1和0。计算概率的最简单的方法就是将它们各自的得分除以它们得分的总和。既为猫的概率是2/3，为狗的概率是1/3，猪的概率是0。 但是这种方法会有个弊端，当得分包含负数会出现这样的情况：1 / (1 + 0 + (-1))，这时候就没法计算概率了。softmax能够把一些输入映射为0到1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。